Electron. J. Diff. Eqns., Vol. 2002(2002), No. 58, pp. 1-13.
Boundary-value problems for the biharmonic equation with a
linear parameter
Yakov Yakubov
Abstract:
We consider two boundary-value problems
for the equation
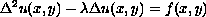
with a linear parameter on a domain consisting of an infinite strip.
These problems are not elliptic boundary-value problems with a
parameter and therefore they are non-standard.
We show that they are uniquely solvable in the
corresponding Sobolev spaces and prove that their
generalized resolvent decreases as
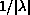 at infinity in
at infinity in
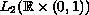 and
and
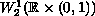 .
.
Submitted April 25, 2002. Published June 18, 2002
Math Subject Classifications: 35J40
Key Words: Biharmonic equation, isomorphism, boundary-value problem.
Show me the
PDF file (256K),
TEX file, and other files for this article.
 |
Yakov Yakubov
Raymond and Beverly Sackler Faculty of Exact Sciences
School of Mathematical Sciences, Tel-Aviv University
Ramat-Aviv 69978, Israel
e-mail: yakubov@post.tau.ac.il |
|---|
Return to the EJDE web page
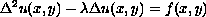
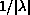 at infinity in
at infinity in
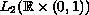 and
and
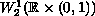 .
.
