Electron. J. Diff. Eqns., Vol. 2002(2002), No. 54, pp. 1-8.
Nonexistence of solutions for quasilinear elliptic equations
with p-growth in the gradient
Darko Zubrinic
Abstract:
We study the nonexistence of weak solutions in
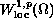 for a class of quasilinear elliptic
boundary-value problems with natural growth in the gradient.
Nonsolvability conditions involve general domains with possible
singularities of the right-hand side.
In particular, we show that if the data on the right-hand
side are sufficiently large, or if inner radius of
for a class of quasilinear elliptic
boundary-value problems with natural growth in the gradient.
Nonsolvability conditions involve general domains with possible
singularities of the right-hand side.
In particular, we show that if the data on the right-hand
side are sufficiently large, or if inner radius of
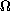 is large, then there are no weak solutions.
is large, then there are no weak solutions.
Submitted April 17, 2002. Published June 11, 2002.
Math Subject Classifications: 35J25, 35J60, 45J05.
Key Words: Quasilinear elliptic, existence, nonexistence,
geometry of domains.
Show me the
PDF file (256K),
TEX file, and other files for this article.
Darko Zubrinic
Faculty of Electrical Engineering and Computing,
Department of Applied Mathematics,
Unska 3, 10000 Zagreb, Croatia
e-mail: darko.zubrinic@fer.hr
Return to the EJDE web page
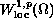 for a class of quasilinear elliptic
boundary-value problems with natural growth in the gradient.
Nonsolvability conditions involve general domains with possible
singularities of the right-hand side.
In particular, we show that if the data on the right-hand
side are sufficiently large, or if inner radius of
for a class of quasilinear elliptic
boundary-value problems with natural growth in the gradient.
Nonsolvability conditions involve general domains with possible
singularities of the right-hand side.
In particular, we show that if the data on the right-hand
side are sufficiently large, or if inner radius of
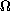 is large, then there are no weak solutions.
is large, then there are no weak solutions.