Electron. J. Diff. Eqns., Vol. 2002(2002), No. 29, pp. 1-13.
Regularity for solutions to the Navier-Stokes equations
with one velocity component regular
Cheng He
Abstract:
In this paper, we establish a regularity criterion for solutions
to the Navier-stokes equations, which is only related to one
component of the velocity field. Let
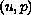 be a weak solution
to the Navier-Stokes equations.
We show that if any one component of the velocity field
be a weak solution
to the Navier-Stokes equations.
We show that if any one component of the velocity field
 ,
for example
,
for example
 ,
satisfies either
,
satisfies either
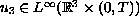 or
or
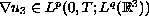
with
 and
and
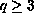 for some positive
for some positive
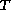 ,
then
,
then
 is regular on
is regular on
![$[0, T]$](gifs/ai.gif) .
.
Submitted November 7, 2001. Published March 17, 2002.
Math Subject Classifications: 35Q30, 76D05.
Key Words: Navier-Stokes equations, weak solutions, regularity.
Show me the
PDF file (265K),
TEX file, and other files for this article.
 |
Cheng He
Department of Mathematics, Faculty of Science
Kobe University
Rokko, Kobe, 657-8501, Japan
e-mail: chenghe@math.kobe-u.ac.jp
On leave from:
Academy of Mathematics and System Sciences,
Academia Sinica, Beijing, 100080, China. |
|---|
Return to the EJDE web page
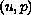 be a weak solution
to the Navier-Stokes equations.
We show that if any one component of the velocity field
be a weak solution
to the Navier-Stokes equations.
We show that if any one component of the velocity field
 ,
for example
,
for example
 ,
satisfies either
,
satisfies either 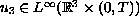 or
or
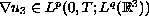
 and
and
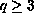 for some positive
for some positive
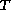 ,
then
,
then
 is regular on
is regular on
![$[0, T]$](gifs/ai.gif) .
.
