We consider a non-local initial boundary-value problem for the equation
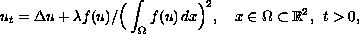
where
 represents a temperature and
represents a temperature and
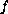 is a positive and
decreasing function. It is shown that for the radially symmetric
case, if
is a positive and
decreasing function. It is shown that for the radially symmetric
case, if
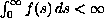 then there exists a critical value
then there exists a critical value
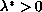 such that for
such that for
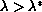 there is no stationary solution and
there is no stationary solution and
 blows up, whereas for
blows up, whereas for
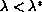 there exists at least one stationary solution.
Moreover, for the Dirichlet problem with
there exists at least one stationary solution.
Moreover, for the Dirichlet problem with
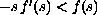 there exists a unique stationary
solution which is asymptotically stable. For the Robin problem, if
there exists a unique stationary
solution which is asymptotically stable. For the Robin problem, if
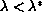 then there are at least two solutions, while if
then there are at least two solutions, while if
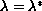 at least one solution.
Stability and blow-up of these solutions are examined
in this article.
at least one solution.
Stability and blow-up of these solutions are examined
in this article.
