Electron. J. Diff. Eqns., Vol. 2001(2001), No. 44, pp. 1-8.
An elementary proof of the Harnack inequality for
non-negative infinity-superharmonic functions
Tilak Bhattacharya
Abstract:
We present an elementary proof of the Harnack inequality for non-negative
viscosity supersolutions of
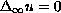 .
This was originally proven
by Lindqvist and Manfredi using sequences of solutions of the p-Laplacian.
We work directly with the
.
This was originally proven
by Lindqvist and Manfredi using sequences of solutions of the p-Laplacian.
We work directly with the
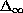 operator using the distance
function as a test function. We also provide simple proofs of the Liouville
property, Hopf boundary point lemma and Lipschitz continuity.
operator using the distance
function as a test function. We also provide simple proofs of the Liouville
property, Hopf boundary point lemma and Lipschitz continuity.
Submitted January 15, 2001. Revised May 17, 2001. Published June 14, 2001.
Math Subject Classifications: 35J70, 26A16.
Key Words: Viscosity solutions, Harnack inequality, infinite harmonic operator,
distance function.
Show me the
PDF file (205K),
TEX file, and other files for this article.
 |
Tilak Bhattacharya
Indian Statistical Institute
7, S.J.S. Sansanwal Marg
New Delhi 110 016 India
e-mail: tlk@isid.isid.ac.in |
Return to the EJDE web page
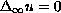 .
This was originally proven
by Lindqvist and Manfredi using sequences of solutions of the p-Laplacian.
We work directly with the
.
This was originally proven
by Lindqvist and Manfredi using sequences of solutions of the p-Laplacian.
We work directly with the
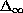 operator using the distance
function as a test function. We also provide simple proofs of the Liouville
property, Hopf boundary point lemma and Lipschitz continuity.
operator using the distance
function as a test function. We also provide simple proofs of the Liouville
property, Hopf boundary point lemma and Lipschitz continuity.
