We show that the well-known non-compact Yamabe equation (of prescribing constant positive scalar curvature) on a manifold with non-negative Ricci curvature and positive scalar curvature behaving like
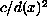 near infinity can not be solved if the volume of geodesic
balls do not increase "fast enough". Even though both existence and
nonexistence results have appeared in the case when the scalar curvature
is negative somewhere([J], [AM]), or when the scalar curvature is positive
([Ki], [Zhan5]), the current paper seems to give the first nonexistence
result in the case that the scalar curvature is positive and
near infinity can not be solved if the volume of geodesic
balls do not increase "fast enough". Even though both existence and
nonexistence results have appeared in the case when the scalar curvature
is negative somewhere([J], [AM]), or when the scalar curvature is positive
([Ki], [Zhan5]), the current paper seems to give the first nonexistence
result in the case that the scalar curvature is positive and
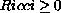 ,
which seems to be the fundamental part of the noncompact Yamabe problem.
We also find some complete non-compact manifolds with positive scalar
curvature which are conformal to complete manifolds with constant
and with zero scalar curvature. This is a new phenomenon which does not
happen in the compact case.
,
which seems to be the fundamental part of the noncompact Yamabe problem.
We also find some complete non-compact manifolds with positive scalar
curvature which are conformal to complete manifolds with constant
and with zero scalar curvature. This is a new phenomenon which does not
happen in the compact case.