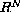
David G. Costa
Abstract:
We consider a class of variational systems in
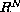 of the form
of the form
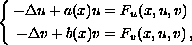
where
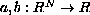 are continuous functions
which are coercive; i.e.,
are continuous functions
which are coercive; i.e.,
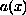 and
and
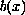 approach plus
infinity as
approach plus
infinity as 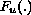 and
and
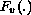 , the (weak) solutions are precisely the critical points
of a related functional defined on a Hilbert space of functions
, the (weak) solutions are precisely the critical points
of a related functional defined on a Hilbert space of functions
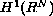 .
.
By considering a class of potentials
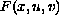 which are
nonquadratic at infinity, we show that a weak version of the
Palais-Smale condition holds true and that a nontrivial solution
can be obtained by the Generalized Mountain Pass Theorem.
which are
nonquadratic at infinity, we show that a weak version of the
Palais-Smale condition holds true and that a nontrivial solution
can be obtained by the Generalized Mountain Pass Theorem.
Our approach allows situations in which
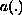 and
and
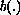 may
assume negative values, and the potential
may
assume negative values, and the potential
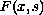 may grow
either faster of slower than
may grow
either faster of slower than
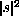
Submitted April 21, 1994. Published September 23, 1994.
Math Subject Classification: 35J50, 35J55.
Key Words: Elliptic systems, Mountain-Pass Theorem, Nonquadratic at
Show me the PDF file (222 KB), TEX file, and other files for this article.